激活函数的发展经历了Sigmoid→Tanh→ReLU→Leaky ReLU等多种不同类型的激活函数及其改进结构，还有一个特殊的激活函数Softmax，它只会被用在网络中的最后一层，用来进行最后的分类和归一化。

Sigmoid激活函数

Sigmoid函数常被用作神经网络的阈值函数，因为它在信息科学中具备单增以及反函数单增等性质，它可以将变量映射至0～1，其公式如下：

$$
f(x)=\frac {1}{1+e^{-x}}
$$

Sigmoid是几十年来应用最多的激活函数之一，它的应用范围比较广泛，值域在0～1，因此可以将其输出作为预测二值型变量取值为1的概率，有很好的概率解释性，Sigmoid激活函数在其大部分定义域内都饱和，仅仅当输入接近0时才会对输入强烈敏感。它能够控制数值的幅度，并且在深层网络中可以保持数据幅度不会出现大的变化。下面是这个函数的图像

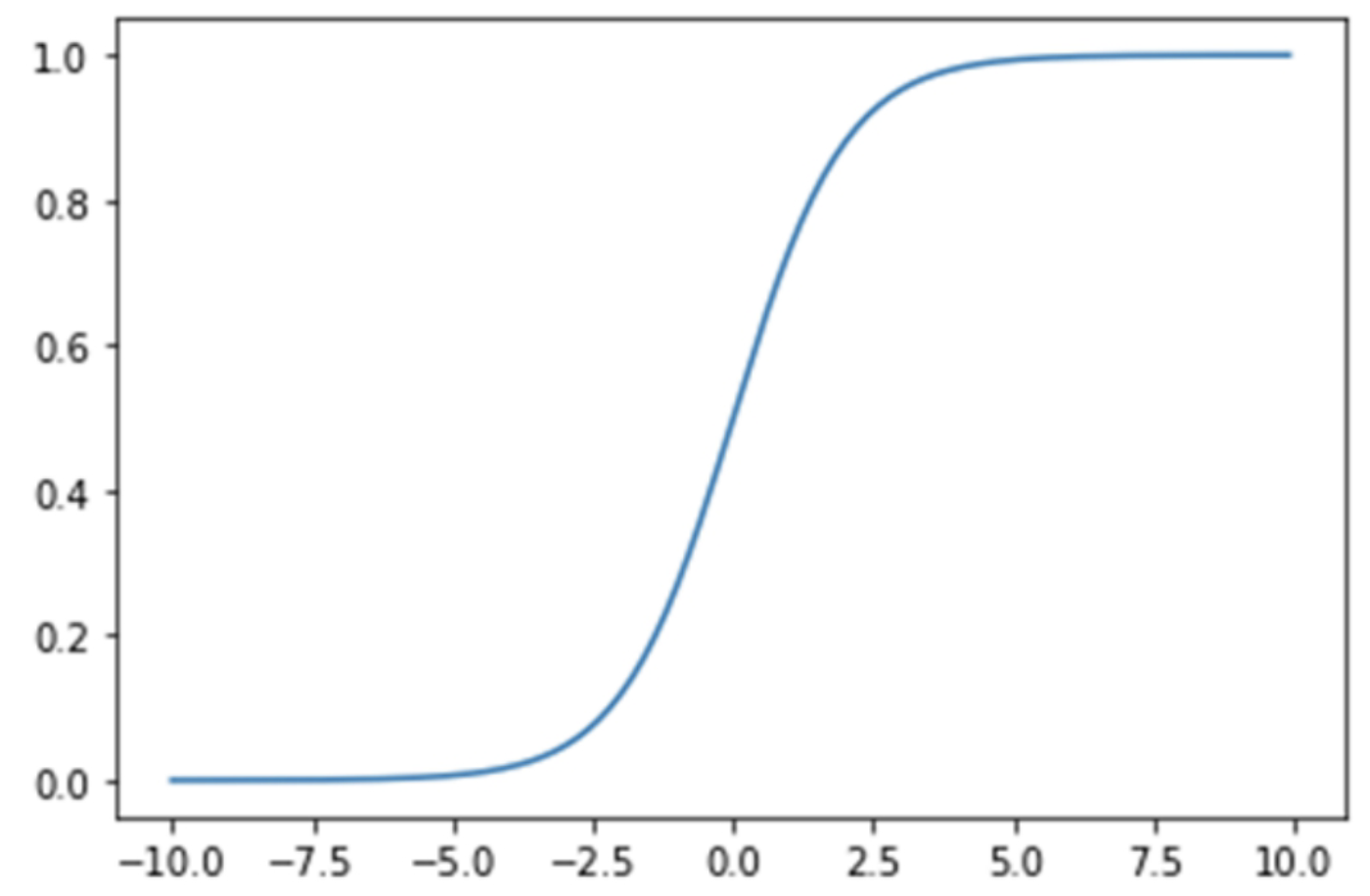
sigmod.png

Sigmoid函数具有明显的优势。首先，Sigmoid函数限定了神经元的输出范围在0～1，在一些问题中，这种形式的输出可以被看作概率取值。其次，当神经网络的损失函数取交叉熵时，S函数可用于输入数据的归一化操作，且交叉熵与Sigmoid函数的配合能够有效改善算法迭代速度慢的问题。

Tanh激活函数

Tanh是双曲函数中的一个，Tanh()为双曲正切。在数学中，双曲正切Tanh是由基本双曲函数双曲正弦和双曲余弦推导而来的，其公式如下：

$$
tanh(x)=\frac {sinh(x)}{cosh(x)}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
$$

分类任务中，Tanh激活函数正逐渐取代Sigmoid激活函数成为神经网络的激活函数。 根据图像可以看出，他关于原点对称，解决了Sigmoid函数中输出值都为正数的问题，而其他属性基本都与Sigmoid函数相同，具有连续性和可微性。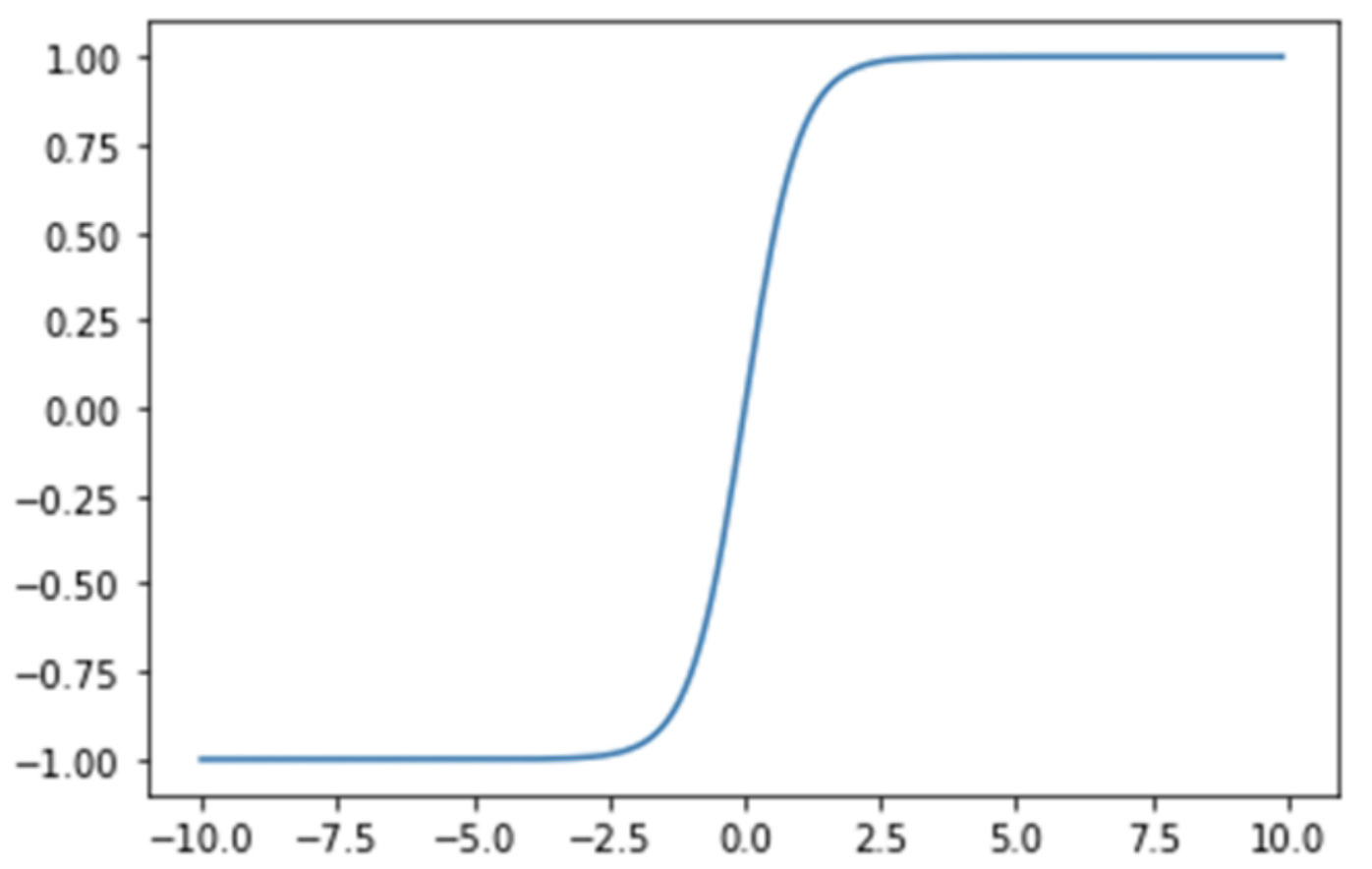
tanh.png

Tanh函数关于原点对称，是一个0均值的函数，这是它较之Sigmod函数有所改进的地方。Sigmoid函数的输出具有偏移现象，即输出均为大于0的实值。而Tanh的输出则均匀地分布在y轴两侧。生物神经元的激活具有稀疏性，而Tanh函数的输出结果更趋于0，从而使人工神经网络更接近生物自然状态。

ReLU激活函数

2001年，线性分段激活函数ReLU（Rectified Linear Unit）首次被提出，伴随深度神经网络的产生而兴起，其公式如下：

$$
f(x)=max(0,x)
$$

ReLU函数的一个直观的特点就是形式简单，抑制所有小于0的输入，仅保留净激活大于0的部分。因此，当x＜0时，函数的导数为0，即ReLU在x轴右侧饱和。但与Sigmoid函数和Tanh函数同时存在左右两个饱和区的情况相比，ReLU陷入单侧饱和的概率已经大大降低。另外，ReLU也是非0均值的激活函数，但是其本身具有的稀疏激活性在一定程度上可以抵消非0均值输出带来的影响。

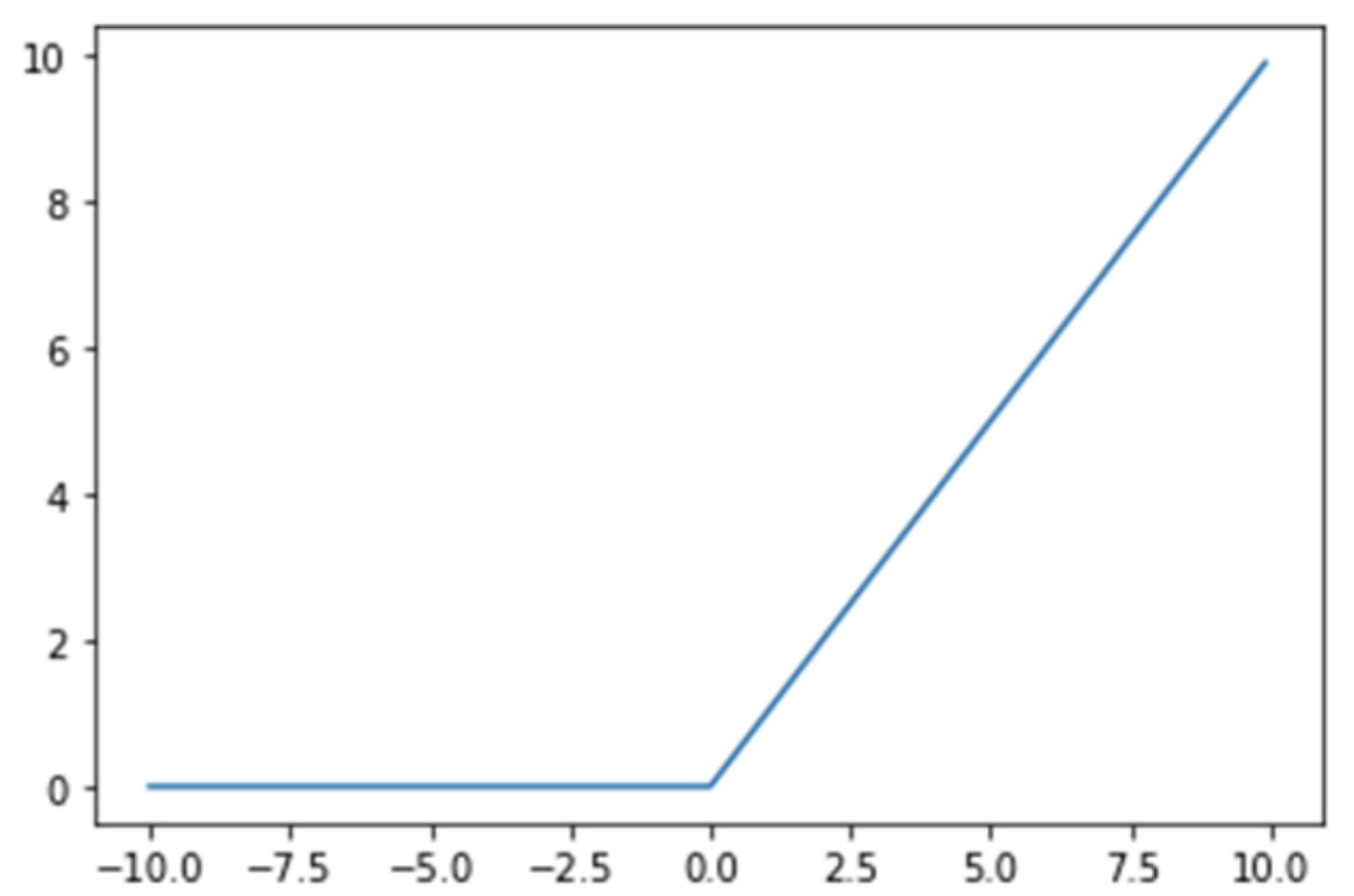
ReLu.png

ReLU函数近年来应用较为广泛，相对于Sigmoid和Tanh，它解决了两个函数存在的致命缺陷，即梯度弥散问题：根据图像不难看出，函数在正无穷处的梯度是一个常量，而不是像前两个函数一样为0，并且由于函数组成简单，运算速度比包含指数函数的Sigmoid以及Tanh要快很多。

Leakey ReLU激活函数

当ReLU的输入值为负的时候，输出始终为0，其一阶导数也始终为0，这样会导致神经元不能更新参数，也就是神经元不学习了，这种现象叫作“神经元坏死”。
为了解决ReLU函数这个缺点，在ReLU函数的负半区间引入一个泄漏（Leaky）值，所以称为Leaky ReLU函数，其公式如下：

$$
f(x)=max(0.01x.x)
$$

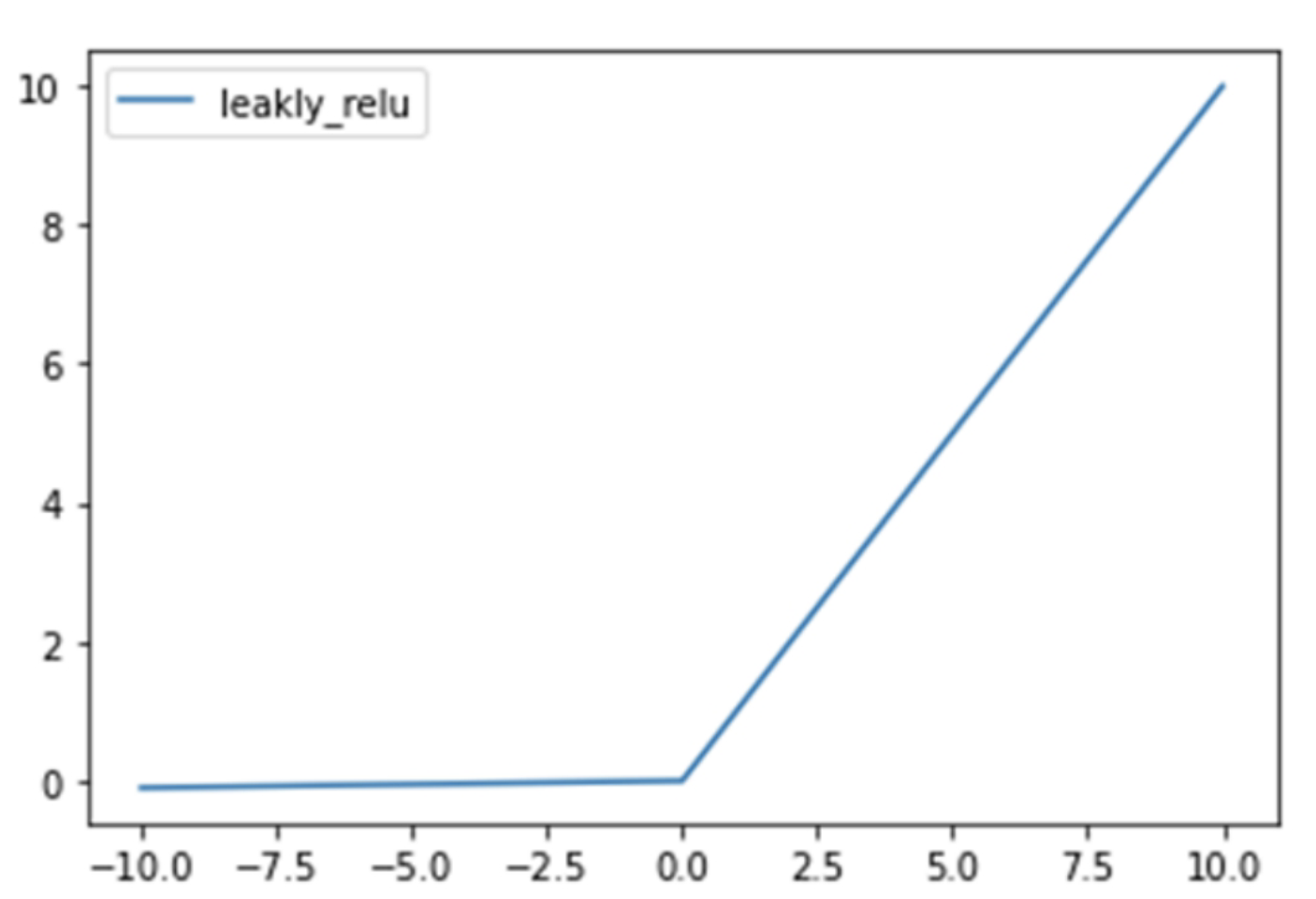
leakrelu.png

带泄漏修正线性单元（Leaky ReLU）函数是经典（以及广泛使用的）的ReLU激活函数的变体，该函数输出对负值输入有很小的坡度。由于导数总是不为零，这能减少静默神经元的出现，允许基于梯度的学习（虽然会很慢），解决了ReLU函数进入负区间后，导致神经元不学习的问题。