ReLU（Rectified Linear Unit，修正线性单元）是深度学习中常用的一种激活函数。它的定义非常简单：

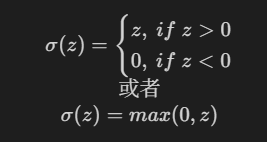
image.png

也就是说，ReLU 函数会将输入中的负值全部置为0，而正值保持不变。

ReLU 函数的图像如下：

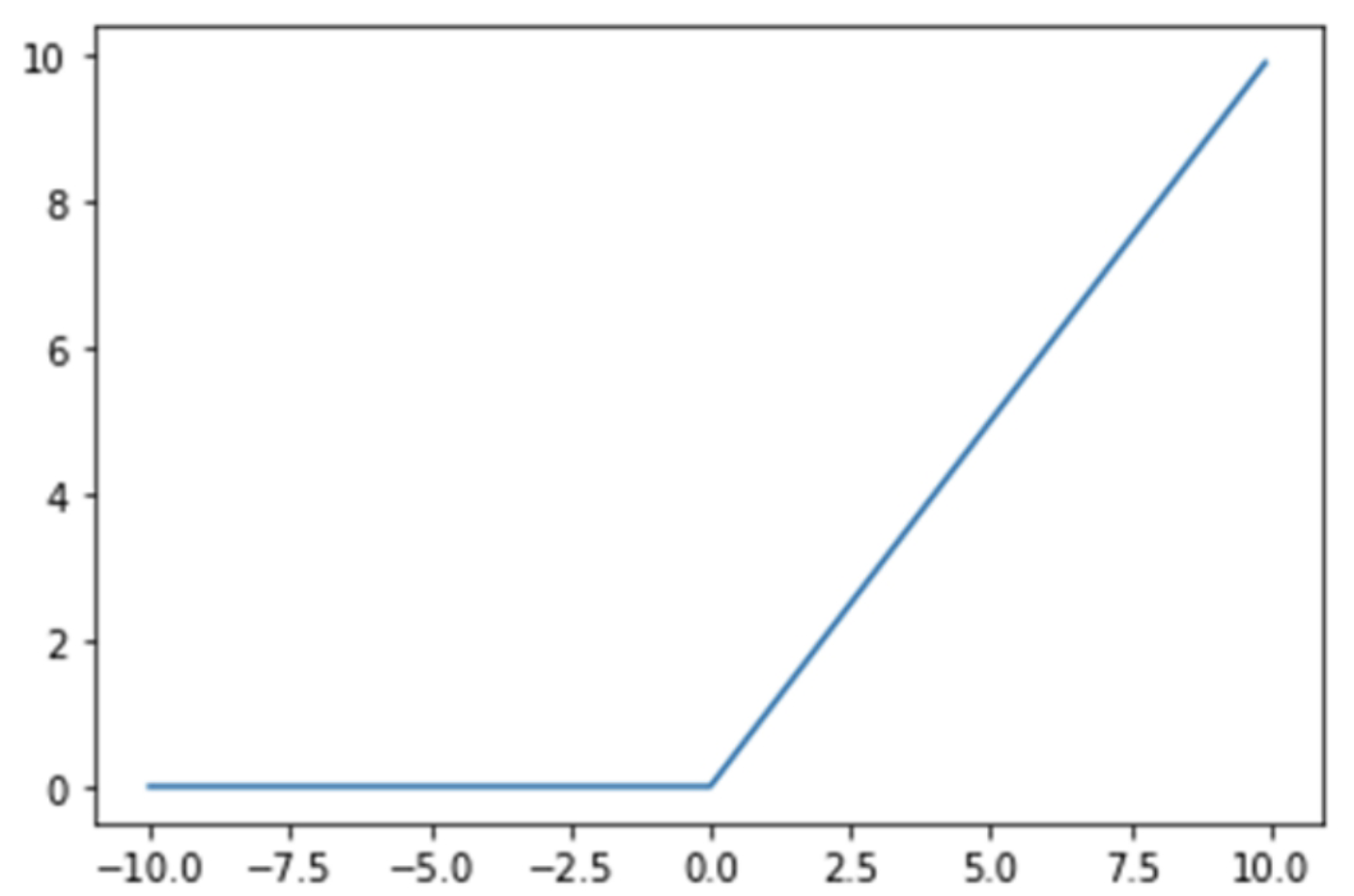
ReLU函数

ReLU 函数的优点包括：

  1. 计算简单：ReLU 函数的计算非常简单，只需要比较输入值和0的大小。
  2. 梯度消失问题：相比于 sigmoid 和 tanh 激活函数，ReLU 函数在正区间的梯度恒为1，能够有效缓解梯度消失问题。
  3. 稀疏激活：ReLU 函数会将一部分神经元的输出置为0，从而引入了稀疏性，有助于模型的泛化能力。

在 PyTorch 中，可以使用 torch.nn.ReLU 或 torch.relu 来应用 ReLU 激活函数。例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
import torch.nn as nn

# 使用 nn.ReLU
relu = nn.ReLU()

# 假设输入张量 x
x = torch.tensor([-1.0, 0.0, 1.0, 2.0])

# 应用 ReLU 激活函数
y = relu(x)

print("输入张量 x:", x)
print("输出张量 y:", y)

输出结果如下：

1
2
输入张量 x: tensor([-1., 0., 1., 2.]) 
输出张量 y: tensor([0., 0., 1., 2.])

在这个例子中，输入张量 x 中的负值被置为0，正值保持不变。

使用 ReLU 的好处是它的梯度要么是 1（对于正值），要么是 0（对于负值）——不再有梯度消失！

这种模式导致网络更快的收敛。 然而，这种行为也可能导致所谓的“神经元死亡”； 也就是说，输入始终为负的神经元，因此激活值始终为零。 更糟糕的是，负输入的梯度也为零，这意味着权重不会更新。 就像神经元被卡住了一样。

ReLU 的激活值显然不是以零为中心。 它会比双曲正切更糟糕吗？ 当然不是，否则它不会成为从业者中如此流行的激活函数。 尽管 ReLU 的输出不以零为中心，但其梯度相对较大，能够比其他两个激活函数获得更好更快的结果。